promise96319

Appearance

红黑树 ​

红黑树 vs AVL树 ​

AVL是严格的平衡二叉树，无论是执行插入还是删除只要不满足要求都会进行旋转，而旋转时非常耗时的，所以AVL树更适合插入和删除比较少但查找多的情况。红黑树是一种弱平衡二叉树，他的旋转次数较AVL少许多，因此应用场景也相对广一些。

性质 ​

  1. 每个结点都是红色的或是黑色的
  2. 根结点是黑色的
  3. 每个叶结点是黑色的
  4. 如果一个结点是红色的，则它的两个子结点都是黑色的
  5. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色节点

插入 ​

  1. 如果父结点为黑色结点，那么插入的红色结点不会影响平衡，跳过。
  2. 如果父结点为红色结点
    1. 如果叔结点为红色结点
      1. 父结点和叔结点变为黑色，祖父结点如果不是根结点则变红色
      2. 向上递归，继续平衡祖父结点
    2. 如果叔结点不存在或是黑色结点
      1. 先进行旋转（同 AVL 树4种旋转方式）
      2. 父结点和祖父节点换颜色
      3. 向上递归，继续平衡祖父结点

删除 ​

  1. 找到替换结点：左子树的最大值结点 or 右子树的最小值结点（类似于二叉查找树的删除结点）
  2. 情景1：如果替换结点是红色，那么直接将替换节点值赋给删除结点，并删除替换结点。
  3. 如果替换结点是黑色：
    1. 情景2：如果替换结点是其父结点的左结点
      1. 情景2.1：如果替换结点的兄弟结点是红色，删除黑结点会导致左侧黑色结点少一，此时通过交换兄弟结点和父结点颜色并向左旋转解决。（类似于右右的结点情况）img
      2. 情景2.2：如果替换结点的兄弟结点是黑色，兄弟结点右结点为红色，左结点为任意颜色，此时不能通过情景2.1那样左旋达到平衡，而是需要将红色右子结点”借“过来。兄弟结点和父结点颜色对调，右子结点变为黑色，并进行左旋。img
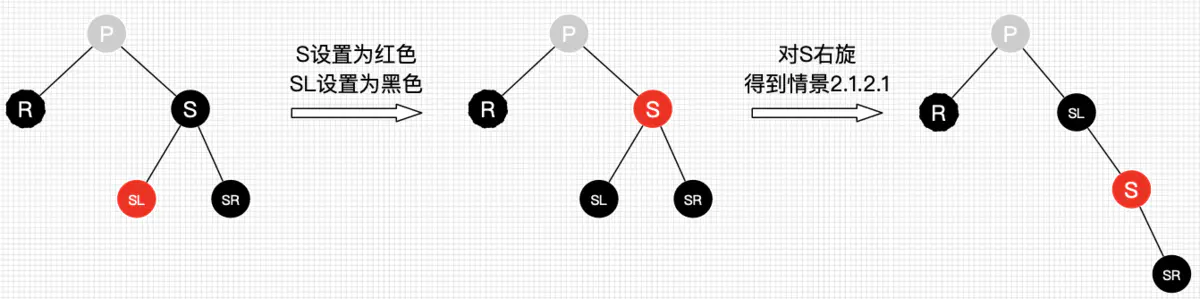
      3. 情景2.3：兄弟结点右结点为黑色，左结点为红色。此时左结点与兄弟结点交换颜色，并右旋。再进行情景2.2img
      4. 情景2.4：兄弟结点子结点均为黑色。此时兄弟结点没有结点可以借了，只能向父结点借，把兄弟结点设为红色，将父结点作为新的替代结点，自底向上处理。 img
    2. 情景3：如果替换结点是其父结点的右结点，与左节点情况镜像

参考 ​